16. Quiz: Mini-Batch Gradient Descent
Programming Quiz for "Mini-Batch Gradient Descent"
Mini-Batch Gradient Descent Quiz
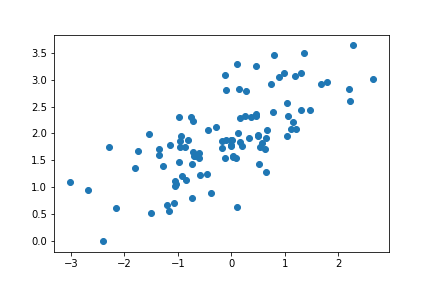
In this quiz, you'll be given the following sample dataset (as in data.csv), and your goal is to write a function that executes mini-batch gradient descent to find a best-fitting regression line. You might consider looking into numpy's matmul function for this!
Start Quiz: